京都医塾数学科です。

このページでは「北里大学医学部の数学」についての過去問分析コメントを紹介します。

・“医学部受験に興味がある”という方
・“北里大学医学部”の受験を考えている方
・“北里大学医学部の数学がどのような問題か知りたい”という方

にオススメの記事となりますので、興味のある方はご一読ください。

概要

【形式・制限時間・配点】2022年度　
形式： 【1】は空所補充、【2】【3】は記述
制限時間： 80分
配点： 150点 / 500点

北里大学医学部の数学は2010年度以降「80分・全3問：【1】（小問集合、空所補充）、【2】【3】（記述）」という形式が続いています。

出題の傾向と特徴（過去5年分）

【毎年恒例の出題単元】

　証明問題が毎年出題されています。2022年と2020年は不等式の証明が出題されており、2019年の証明は一見すると極限の問題ですが、極限が収束することを示すために不等式を証明する必要があります。いずれも典型的な出題ですが、初見で解くのは難しいため、きちんと対策を立てる必要があります。
　また、数学Ⅰ「データの分析」は出題されないことが募集要項に明記されています。

【頻出の出題単元】

　小問集合では複素数平面が毎年出題されており、そのほかでは微分法・積分法、ベクトル、整数が頻出です。微分法・積分法は接線や面積・体積に関する問題が多く出題されています。
　大問では場合の数・確率、微分法・積分法、極限が頻出です。これらは前述のとおり証明問題が絡んでくることもあり、難易度は軒並み高めとなっています。また、場合の数・確率は漸化式と融合されて出題されることが増えてきています。

【制限時間に対する問題量】

　80分で3問と、一見余裕のある時間設定ですが、小問集合の計算量が多く、大問では証明問題をはじめとして記述すべき量が多いため、全問きちんと解こうとするとかなりの処理能力が問われます。問題を見たらすぐに解法が浮かぶ程度に基礎知識を定着させておく必要があります。

2022年度（最新の過去問）の分析

さらに踏み込んで、最新の入試問題を具体的に分析したいと思います。

※以下、過去問をお手元にご覧になるのが理想的ですが、過去問がなくても問題なくお読み頂けます。

【第１問　小問集合】（難易度：(1)と(3)はやや易、(2)と(4)は標準）　

(1) … 複素数平面
　(ア) … 複素数の \(n\) 乗なので、「絶対値は \(n\) 乗、偏角は \(n\) 倍」として求めましょう。
　(イ) … \(z,\overline{z}\) のまま計算してもよいですし、 \(z=x+yi\) を代入してもよいでしょう。

(2) … 関数、方程式の解の個数
　(エ) … 逆関数の性質が分かっていれば難なく埋められます。
　(オ) … 「方程式の解の個数 = グラフの共有点の個数」であることを利用しましょう。\(f^{-1}(x)\) の値域は、元の関数である \(f(x)\) の定義域と一致することを忘れずに。
　(カ) … 一見複雑に見えますが、\(f^{-1}(x)=t\) とおくと、「\(2\) 次方程式の解の配置」の問題になります。

(3) … 整数、数列、集合
　(キ) … 典型的な \(1\) 次不定方程式ですね。解を \(1\) 組見つけて変形していきましょう（見つけにくい場合は、ユークリッドの互除法を用いて見つけましょう）。
　(ク) … \(A\) の要素の総和と\(B\) の要素の総和を足したものから、\(A\) かつ \(B\) の要素の総和を引いて求めることになります。\(A\) かつ \(B\)は、「\(30\) の倍数かつ \(23\) で割ると \(4\) あまる数」なので、まず

\(30m=23l+4 （m,n\)は整数）

として一般項を求めるところから始めるとよいでしょう。このときに(キ)の結果が使えます。
　(ケ)～(シ) … まず

\(\sqrt{m^2+120} = k　（k\)は整数）

とおき、両辺を\(2\)乗します。その後、因数分解して答えを出すことになります。

(4) … 微分・積分
　(ス) … 微分して接線の傾きを求めたのち、「\(2\) 直線が垂直 \(\Rightarrow\) 傾きの積が \(-1\)」であることを用います。
　(セ) … 「\(\displaystyle \frac{1}{12}\) 公式」と呼ばれる公式を使えば一瞬で埋まりますが、覚えていない人がほとんどだと思いますので、地道に積分計算をしましょう。\(2\) 直線の交点で積分区間を分ける必要があることに注意しましょう。また、\(x=p,x=q\) で放物線と直線が接することから、被積分関数は必ず \((x-p)^2,(x-q)^2\) の形になります。この形にしないとかなり面倒な計算を強いられますので、必ず変形しておきましょう。
　(ソ) … 長方形 \(\mathrm{PRQS}\) の面積を \(U\) とすると、\(S+T=U\) が成り立ちます。\(U=2 \times \triangle{\mathrm{ABC}}\) であることから \(T\) を求めると、

\(\displaystyle T=\frac{5}{12} \left( p+\frac{1}{4p} \right)^3\)

となります（\(\triangle{\mathrm{ABC}}\) の面積は、面積公式 \(\displaystyle S=\frac{1}{2}|a_1b_2-a_2b_1|\)で求めます）。微分して最小値を求めてもよいですが、かっこの中身が逆数の和の形になっているので、相加・相乗平均の関係を使うのが良いでしょう。

≪2022年度の目標≫

数学を得点源にしたい受験生…完答。

他教科を得点源にしたい受験生…できれば完答だが、最低でも(1)と(3)は確保。(2)(4)も最初の空欄までは埋めたい。

【第２問　不等式の証明】（難易度：(1)は易、(2)(3)はやや難）

(1) … \(x=\tan{\theta}\) とおく典型的な置換積分です。

(2) … \(e^x>1+x　\cdots　\)① は、\(f(x)=e^x-x-1\) とおき、与えられた範囲 (\(x \neq 0\)) でつねに \(f(x)>0\) となることを示します。\(f(x)\) を微分し、増減表を書いて示しましょう。
　\(\displaystyle e^{-x^2}<\frac{1}{1+x^2}\) は、先ほどと同じように示そうとするとうまくいきません。そこで、式を少し変形してみると、

\(\displaystyle e^{-x^2}<\frac{1}{1+x^2}　\Rightarrow　\frac{1}{e^{x^2}}<\frac{1}{1+x^2}　\Rightarrow　e^{x^2}>1+x^2\)

となり、①の \(x\) に \(x^2\) を代入したものになっています。証明するときはまず①に \(x^2\) を代入し、上の流れを逆にたどっていけばよいでしょう。

(3) … (2)より、\(\displaystyle e^{-x^2}<\frac{1}{1+x^2}\) であることはわかっているので、両辺を \([0,1]\) の範囲で積分すれば、不等式の右半分は証明できます。
　左半分を示すためには、もう一つ新しい式が必要になります。今度は、①の \(x\) に \(-x^2\) を代入してみましょう。このように、最終的に必要な式の片方だけは誘導で導いてくれるが、もう一つは自力で導かなければならない、ということは入試ではよくあります。

≪2022年度の目標≫

数学を得点源にしたい受験生…完答。

他教科を得点源にしたい受験生…(1)まで。

【第３問　確率】（難易度：(1)(2)は易、(3)は標準、(4)は難）

(1)、(2) … いわゆる「確率漸化式」の問題です。まず \(a_n + b_n = 1\) より \(b_n=1-a_n\) がわかります。確率漸化式の問題は「\(n\) 回目と \(n+1\) 回目に着目する」ことが定石です。以下のような「状態推移図」にまとめるとよいでしょう。

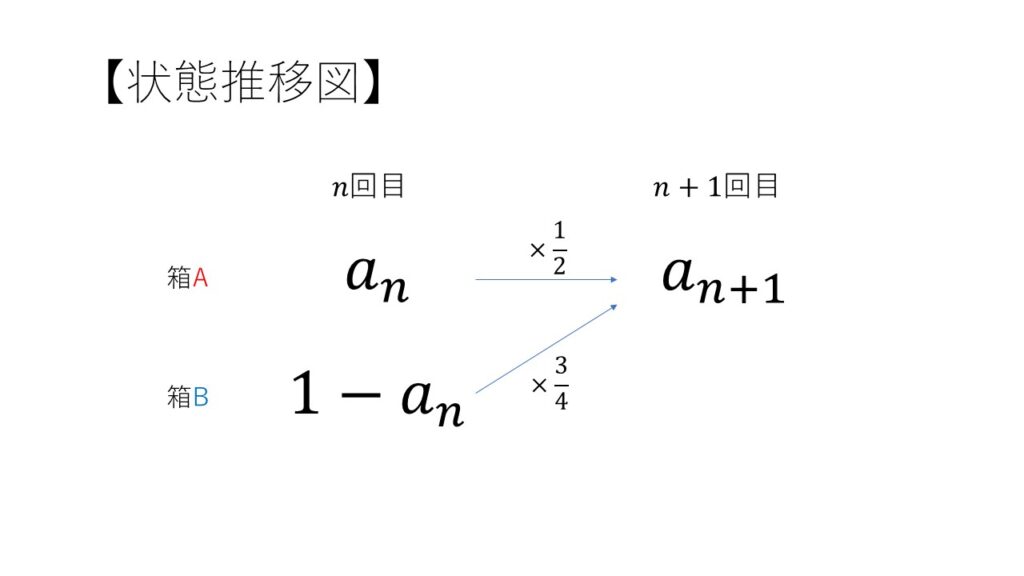
あとは、求めた漸化式を解くだけとなります。

(3) … たとえば、最初からずっと赤玉を引き続ければ、台の上には箱 \(\mathrm{A}\) が置かれたままになるので、白玉を引くことはありません。途中何回目かで青玉を引くと、台の上には箱 \(\mathrm{B}\) が置かれます。そのあとは青玉を引き続ければ条件を満たしますね。ということで、「\(k-1\) 回目までは箱 \(\mathrm{A}\) から赤玉を引き、\(k\) 回目は箱 \(\mathrm{A}\) から青玉を引き、\(k+1\) 回目から \(n\) 回目までは箱 \(\mathrm{B}\) から青玉を引く」という確率を \(c_k\) とし、\(\displaystyle \sum_{k=1}^n c_k\) を求めます。これに、「箱 \(\mathrm{A}\) から白玉を \(n\) 回引き続ける」確率を足せば、答えとなります。

(4) … \(k\) 回目に白玉を引いたとすると、残りの \(n-k\) 回は \(1\) 度も白玉を取り出さないので、(3)の結果を用いることができそうです。ただし、\(k\) 回目に白玉を引くためには、 \(k\) 回目の時点で台に箱 \(\mathrm{B}\) が置かれている必要があります。そのほか、定数 \(k\) の範囲を考える必要がある、計算が煩雑である、といったことより、(4)は捨てて、ほかの問題に時間を割いた方が良いかもしれません。ほかの問題もすべて解き終わり、時間に余裕があるなら解いてみる、といったバランスで取り組むのが良いでしょう。

≪2022年度の目標≫

数学を得点源にしたい受験生…(3)まで。

他教科を得点源にしたい受験生…(2)まで。できれば(3)も。

【総評】

　【1】は標準的な問題が並びますが、【2】【3】は経験によって差がつく出題となっています。数学に自信のない人は、とにかく【1】は取りこぼさないようにし、【2】【3】も前半部分は取れるようにしておく必要があります。数学でアドバンテージを取りたい人は、頻出分野である「不等式の証明」「微分法・積分法」「確率」の演習を行い、融合して出題されやすい漸化式の立式・処理についても経験を積むとよいでしょう。

≪2022年度の目標≫

数学を得点源にしたい受験生…8.5割

他教科を得点源にしたい受験生…6割

まとめ

今回は北里大学医学部の数学についてまとめてみました。皆さんの参考になれば幸いです！

京都医塾ではご相談・体験授業を随時募集しています。下記リンクからお気軽にお問い合わせください。