皆さんこんにちは。京都医塾数学科講師の田村がお送りします。
突然ですが、皆さんは数学Ⅲの極限は得意ですか?公式が多くある、式変形が多岐にわたる、などの理由で苦手としている人がたくさんいる事かと思います。また、「無限」という概念が今ひとつピンとこない、という人もいるのではないでしょうか?
今回はそんな「無限」のちょっと不思議な話をご紹介していきたいと思います。
無限を扱うときに現れる”不思議”
極限の勉強をしていると、「無限等比級数」という単元に出会うことになると思います。詳しい説明は避けますが、これは等比数列を無限に足し合わせたもの、つまり
\(1 + \displaystyle \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \cdots \)
というものです。こちらも詳しい説明は避けますが、この和は \( 2 \) に収束することが知られています。「無限に足し合わせているのに、有限の値に収束する」って、結構不思議じゃないですか?
このように、「無限」を扱うと直感に反する不思議なことが起こることがあります。今回はそんな不思議の代表格、「ガブリエルのラッパ」というものを紹介します。
ガブリエルのラッパとは
そもそもガブリエルのラッパってなんやねんって話ですが、元となったのは「旧約聖書で大天使ガブリエルが最後の審判のときに鳴らすラッパ」だそうです。知らんけど。
数学的には、「\( \displaystyle y = \frac{1}{x} \) の \(x ≧ 1\) の部分と \(x\) 軸で囲まれた領域を、\(x\) 軸の周りに回転させてできる立体」の事を指します。言葉で書かれても良く分からないと思うので、下図をご覧ください。
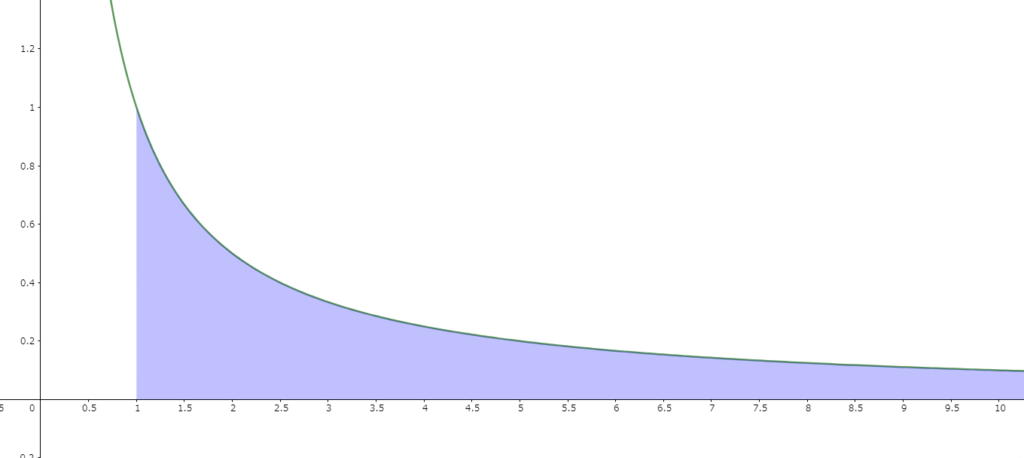
この図の色がついている部分を \(x\) 軸の周りに回転させたときにできる立体がガブリエルのラッパです(見やすさのため、\(x\) 軸と \(y\) 軸の比率を変えています)。図では途切れていますが、右側に無限に広がる領域となります。また、出来上がる立体のイメージ図は下図のようになります。名前の通り、細長いラッパのような形ですね。
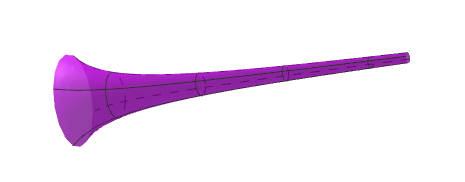
この立体は、「断面積は無限大に発散するが、体積は有限の値に収束する」という不思議な性質を持っています。このことを今から確認していきましょう。
実際に求める
まずは断面積から
図1の面積を2倍すればよいですね。いきなり求めようとすると積分区間が \(1 ~ \infty\) となってしまうので、一旦区間の上端を \(a\) とし、面積を \(a\) の式で表した後で \(a\) を無限大に飛ばす、という流れで求めてみましょう(この計算は「広義積分」という名前がついており、詳しくは大学の数学で学びます)。
断面積を \(S\) とすると、
\( S = \displaystyle 2\int _1^a \frac{1}{x} dx = 2\biggl[\ \log |x| \ \biggr]_1^a = 2\log a \longrightarrow \infty (a \rightarrow \infty\)のとき\( ) \)
となり、断面積は発散することが分かります。
続いて、体積
積分区間は断面積のときと同じように設定します。
体積を \(V\) とすると、
\(\displaystyle V = \pi \int_1^a \left( \frac{1}{x} \right)^2 dx = \pi \int_1^a \frac{1}{x^2} dx = \pi \left[\ – \frac{1}{x}\ \right]_1^a = \pi \left(1-\frac{1}{a} \right) \longrightarrow \pi (a \rightarrow \infty\)のとき\( )\)
となり、体積は有限の値 \(\pi\) に収束することが分かります。
以上より、ガブリエルのラッパが「無限の断面積」と「有限の体積」を併せ持つことが証明できました。実はこのガブリエルのラッパ、断面積だけでなく表面積も無限大に発散することが知られています。回転体の表面積を積分で求める問題は高校数学ではなかなかお目にかかる機会はありませんが、興味のある人はぜひ証明してみてください。
まとめ
このように、「無限」というものを扱うと、我々の想像を超える結果が生まれることがあります。苦手な人にとって数学の勉強は苦痛そのものかもしれませんが、普段の学習の中でもこのような”不思議”を探し、解決していけばきっと楽しいものに変わると思います。
また、前項で述べた「断面積が発散することが分かった→じゃあ表面積はどうだろう?」というように、一つのことが分かったらまた別の疑問を持つ、ということが数学に限らずあらゆる教科の学習で非常に重要になります。問題演習で1問解けたら「あ、できた!」で終わるのではなく、「じゃあこういう場合はどうなるだろう?」といった視点を持てるように、常にアンテナを張り続けるようにしていきましょう。


