京都医塾数学科の井上です。
今回は数学の試験で1点でも多く取り切るために、ちょっとしたヒントをいくつか挙げてみたいと思います。
マーク式試験において
マーク式では、とにかく「空欄は作らない」という事が大切です。例えば、1桁の数を埋める空欄であれば適当に塗っても \(\frac{1}{10}\)(10%)の確率で正答できます。
ただし、「当てずっぽうで適当にマークしなさい!」と言いたいわけではありません。
10通りまで絞れたわけですから、具体的に代入して成り立つかどうか確認するという方法があります。
例 1
\(3e^{2x}-7e^{x}=6\) であるとき,\(e^{kx}=243\)を満たすk はアである。(藤田医科大学2021)〈代入を利用した解法〉
\(k=0\)とすると、\(e^{kx}=1\)(≠243) となるので、明らかに不適。
\(k=1\)とすると、\(e^{x}=243\)であり、条件式の左辺は \(3・243^{2}-7・243\)となる。
この値は右辺:6より明らかに大きいため、不適。
(同様に調べていくと…)
\(k=5\)とすると、\(e^{5x}=243\) となり、\(e^{x}=3\)である。
条件式の左辺は3・3^2-7・3= 6 となるため、これが解である。
(実際は、\(243=3^{5}\) であることに気付けば最初から \(k=5\) と予想することもできます。)
また、特定の形であれば、更に絞る事ができます。
例2
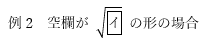
この場合であれば0・1・4・8・9は入らないはずなので、適当に埋めても正答率は20%に上がります。
更に、この空欄が三角比・三角関数絡みの問題だったとすると、有名角の三角比を考えると2または3である可能性が非常に高くなります。
例3
例3 \(\vec{a}・\vec{b}\) = ウ であるから~ベクトルの内積の結果が1桁の整数である、と分かっている状態です。
「(内積)=0」より「直交」と分かる(※)、という典型的な展開が予想できるため、計算方法が見えなかったり時間が無くても、とりあえず “ 0 ” を入れておきましょう。
※数学的な正確さに欠ける書き方になっていますが、あくまでも空欄を埋めるテクニックとして紹介しています。(ここでは細かい説明は省略します。)
記述式試験において
マーク式試験とは違い、空欄の形からヒントを得ることはできませんが、違った観点から「1点でも多く取りに行く」という事は出来ます。
1つ目の戦略は、「証明問題はヒントに使って、次の問題を解く」です。
例4
2次方程式\(4x^{2}+2x-1=0 \)の2つの解を\(α,β(α>β)\)とする。
(1) \(α=cosθ\) となる角\(θ\)が,\(\frac{π}{3}≦θ≦\frac{π}{2}\)の範囲に1つだけ存在することを示せ。
(2) (1) の\(θ\)について,\(β=cos2θ\) が成り立つことを示せ。
(3) (1) の\(θ\)を求めよ。
(2013 東北大)
証明問題が(1)にあるので、一旦諦めて次の大問に移るという受験生もいるのではないかと思います。
しかし、証明を飛ばして後の小問を解いてはいけないという決まりはありません。しかも、(3)は「(1)(2)で証明したことを使え」という流れの問題だと考えられるので、(1)(2)が成り立ったという前提で解けばよいのです。
実際に、(3)だけならば2解を \(α=cosθ,β=cos2θ \)として「2次方程式の解と係数の関係」を用いて条件式を2つ立てて解くだけです。
ちなみに、(3)の解は \(θ=\frac{2}{5}π\) です。
次に紹介するのは、「解き方が分からなくても予想してみる」です。
例 5
\(a_{1}=\frac{1}{3} , a_{n+1} = \frac{1}{2-a_{n}}\)で定められた数列 \(a_{n}\)の一般項を求めよ。
分数型漸化式と呼ばれるパターンの1つですが、誘導無しで出題されると難易度は高くなります。( 両辺逆数を取る、ではうまくいかない事は分かると思います。 )
何をしてよいか分からないから白紙、となってしまいそうですが、少しでも点を取るにはどんな戦略が考えられるでしょうか。
漸化式は、「ドミノ倒し」に例えられるように、「ある項が判明していればその次の項が求まる」という仕組みになっています。
そのため、漸化式に\(n=1\) を代入すると\(a_{2}= \frac{1}{2-a_{1}}\) より、\(a_{2}=\frac{3}{5}\) と分かります。
同様に、\(n=2\)を代入することで\(a_{3}=\frac{5}{7}\) 、\(n=3\)を代入することで \(a_{4}=\frac{7}{9}\)と続きます。
\(a_{1}=\frac{1}{3}\) ,\(a_{2}=\frac{3}{5}\),\(a_{3}=\frac{5}{7}\) ,\(a_{4}=\frac{7}{9}\)a … と並べると、\(a_{n}=\frac{2n-1}{2n+1}\) と予想することができます。
答えだけを記入するタイプであればこれをそのまま書けばよいのですが、記述式であればその予想が正しい事を示す必要があります。
証明が難しい、または解く時間が無い時は、
〈答案〉
一般項を \(a_{n}=\frac{2n-1}{2n+1}\) と予想し、これを数学的帰納法によって証明する。
n=1の時は明らかに成り立つ。
以上を書くだけで、部分点を期待できます。
まとめ
ここまで、「最後まで1点でも多く取りに行く」という戦略についてお伝えしました。
ただ、今回ご紹介したものは、所詮小手先のテクニックにすぎません。優先すべきなのは王道の解法です。どうしても解法が見えてこない、公式などをど忘れした、見直しも一通り済んだけれどまだ時間がある、といった状況で使ってみて下さい。


